Encontrar puntos alineados
Imaginemos que tenemos un mapa del cielo estrellado, y queremos encontrar una hipotética constelación para la cual sabemos que todas sus estrellas están alineadas formando una línea recta. En este post veremos y compararemos diferentes formas de automatizar esta búsqueda.
Contenidos
- El análisis de imágenes
- Descripción del problema
- Método 1: Áreas de triángulos
- Método 2: Agrupar por ángulo
- Codificación
- Materiales
El análisis de imágenes
La visión artificial o computer vision es una disciplina que intenta obtener datos a través de imágnes que puedan ser procesados por un ordenador. El procedimiento de análisis de imagen comprende diferentes etapas, algunas de ellas son:
- Extracción o adquisición de la imagen.
- Preprocesamiento: Consiste en aplicar diferentes tratamientos a una imagen con el fin de eliminar ruido o realzar características interesantes para el posterior análisis.
- Segmentación: Obtención de características útiles de la imagen.
- Reconocimiento: Consiste en interpretar los datos obtenidos y darles un significado.
Esta última tarea (generalmente la más sofisticada del proceso) es la que trataremos en el post, con un ejemplo muy sencillo, la obtención de los puntos alineados o colineares en una imagen.
Descripción del problema
Supongamos que hemos obtenido un conjunto de puntos sobre una imagen (es decir, un conjunto coordenadas x y sus correspondientes coordenadas y). Nuestra tarea consiste en encontrar grupos de 3 o más puntos que estén alineados, es decir, puntos por los cuales pasa una misma recta.
Método 1: Áreas de triángulos
Es claro que dos puntos siempre definen una única recta que pasa por ambos. ¿Ocurre lo mismo para cualquier número de puntos? No, en general, tres o más puntos definen un polígono en el plano. Nosotros nos centraremos en el caso de tres puntos. Tres puntos por tanto definen un triángulo. Conociendo el área de este triángulo podemos comprobar si los puntos están alineados fácilmente, ya que el área debe ser nula.
Por tanto, para este primer método propuesto podemos escoger cada terna de puntos y hallar el área del triángulo que definen. Si el área es cero habremos encontrado tres puntos alineados. Podemos hacernos una idea de cómo funciona el proceso observando la siguiente animación:

En la sección de Codificación veremos cómo implementar este método en lenguaje Python.
Coste teórico
El algoritmo que acabamos de describir tiene un problema y es el elevado número de combinaciones posibles que debemos analizar. Para cada punto del conjunto inicial debemos probar con cada uno de los puntos restantes y para cada uno de ellos con los restantes de nuevo. Es decir, si tenemos puntos el número de veces que calcularemos el área será:
Obtenemos un coste cúbico el cual se dispara para valores muy grandes de . En caso de que quisiéramos encontrar $p$ puntos alineados el coste sería , es decir, el algoritmo sería muy poco eficiente. Este resultado era de esperar, ya que estamos usando un método de fuerza bruta (probar todas las combinaciones posibles de puntos).
Método 2: Agrupar por ángulo
Este interesante enlace de la universidad de Princeton plantea un método quizá no tan visual e intuitivo pero sin duda mucho más eficiente.
Consiste en lo siguiente: escogemos un punto de referencia dentro del conjunto. Una vez escogido calculamos, para cada punto restante, el ángulo que forma el eje con la recta que pasa por este punto y el de referencia. Una vez disponemos de esta lísta de pares solo nos queda ordenar esta lista en función del ángulo. Fácilmente podremos detectar los puntos alineados, ya que serán los grupos de dos o más puntos que compartan el mismo ángulo.
Éste algoritmo se puede aplicar a cada uno de los puntos del conjunto para obtener todas las rectas generadas.
En la sección de Codificación veremos cómo implementar este método y cómo definir el ángulo correctamente.
Coste teórico
Para este algoritmo la parte que conlleva más esfuerzo es la ordenación de la lista de ángulos. Para ello hay diferentes algoritmos pero supondremos uno de coste , que de hecho es el coste del algoritmo de ordenación de listas por defecto en Python.
Por tanto, aproximadamente el coste total sería:
Ya que hay que repetir el proceso veces, una por cada punto. Este método es mucho más eficiente en comparación con el anterior por fuerza bruta.
Codificación
Implementaremos ambos métodos, comprobaremos sus resultados y por último compararemos sus tiempos de ejecución para diferentes tamaños del conjunto de puntos de entrada.
En esta ocasión utilizaremos la librería pyplot de matplotlib para realizar las gráficas donde visualizaremos los puntos que generaremos y las rectas que encontremos. Para generar puntos aleatorios utilizaremos la librería numpy. Además utilizaremos la librería time para calcular los tiempos de ejecución.
La última línea del siguiente bloque de código sirve para agrandar el tamaño de los gráficos que generemos con pyplot.
import time
import numpy as np
from matplotlib import pyplot as plt
plt.rcParams["figure.figsize"] = (7,7)
Sorteando los puntos
Generamos una lista con todas las coordenadas X de los puntos y otra para las coordenadas Y.
Opcionalmente, creamos una lista de valores para asignar un color a cada punto. En este caso utilizaremos la suma de coordenadas para más adelante mapear estos valores con los colores codificados en modo HSV. De esta forma obtenemos un efecto “arcoiris” en la visualización.
n_points = 50 # Number of points
# Creating a random set of points
x_values = [np.random.randint(100) for i in range(n_points)]
y_values = [np.random.randint(100) for i in range(n_points)]
colors = [x_values[i] + y_values[i] for i in range(n_points)]
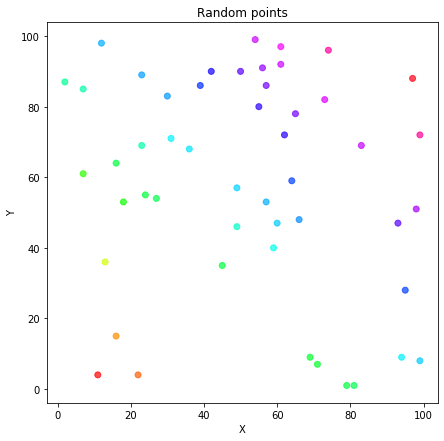
Visualizamos los puntos para comprobar que se han creado correctamente.
# Plot
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Random points')
_ = plt.scatter(x_values, y_values, c=colors, cmap='hsv', alpha=0.7)
plt.show()
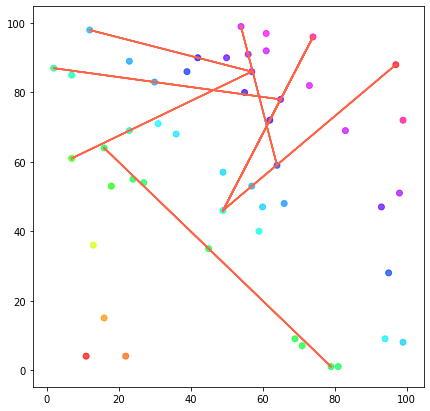
Método 1: Área del triángulo
Implentamos el primer método que comentábamos más arriba. Podemos observar el triple bucle anidado que nos indica el coste del que hablábamos. La función devolverá dos listas de coordenadas X y Y, que tomadas de dos a dos definirán los segmentos que formen las rectas buscadas.
def colinear_1(x_values, y_values):
size = len(x_values)
x_segments = []
y_segments = []
for i in range(size):
x1, y1 = x_values[i], y_values[i]
for j in range(size):
if i == j:
continue
x2, y2 = x_values[j], y_values[j]
for k in range(size):
if i == k or j == k:
continue
x3, y3 = x_values[k], y_values[k]
# Comprobamos si el area es nula
if x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2) == 0:
x_segments += [x1, x2, x1, x3]
y_segments += [y1, y2, y1, y3]
return x_segments, y_segments
Una vez definida la función la aplicamos a los puntos generados anteriormente y comprobamos el resultado.
x, y = colinear_1(x_values, y_values)
# Showing the results
for i in range(0, len(x), 2):
_ = plt.plot(x[i:i + 2], y[i:i + 2], c='Tomato', alpha=0.7)
_ = plt.scatter(x_values, y_values, c=colors, cmap='hsv', alpha=0.7)
plt.show()
Método 2: Agrupar por ángulo
Veamos cómo implementar el segundo método. El paso crucial para que este algoritmo funcione es definir correctamente la función ángulo.
Definiendo el ángulo
Intentemos definir el ángulo de manera rápida. Fijémonos en la siguiente figura:
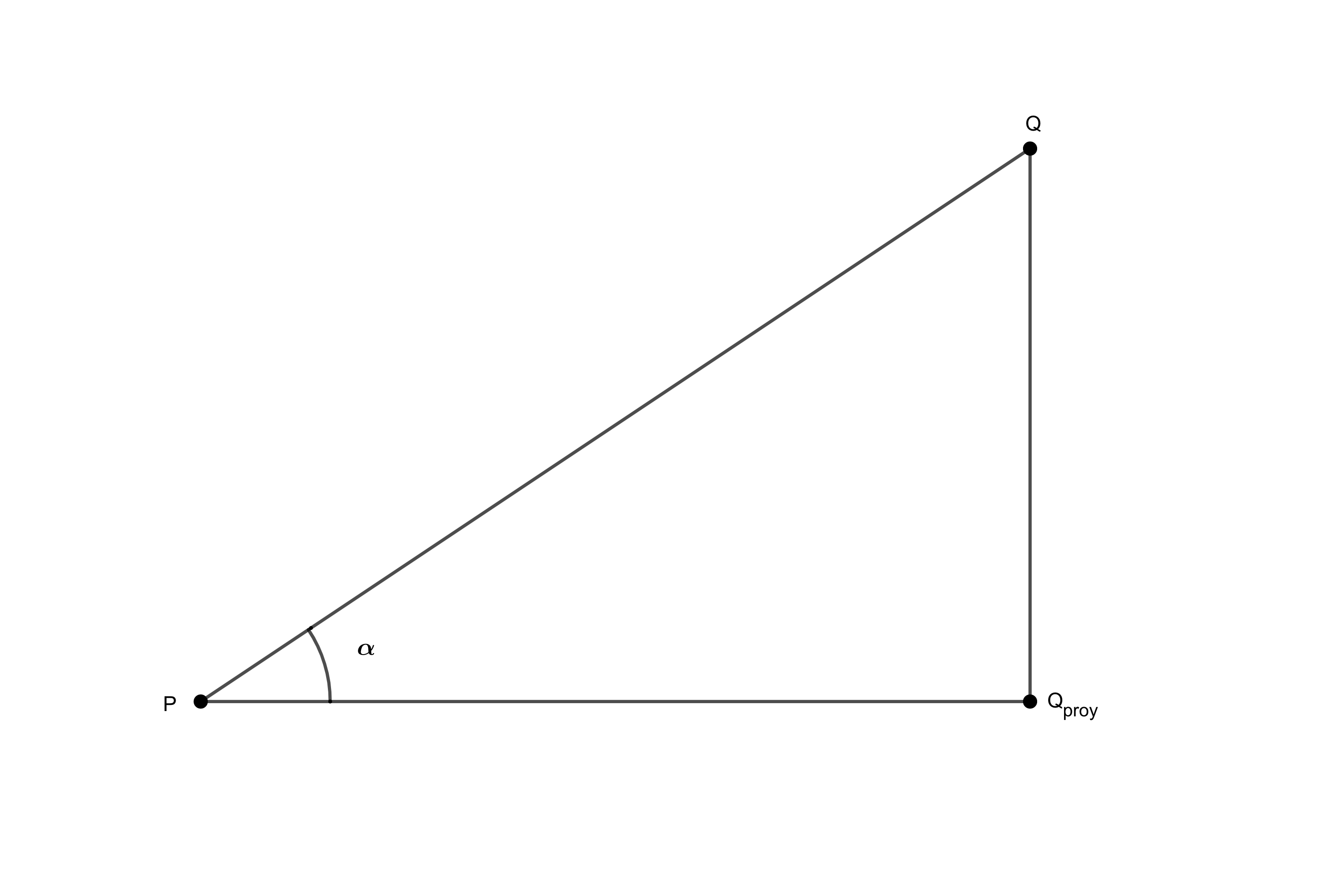
Si queremos obtener el ángulo $\alpha$ formado por el segmento y el eje facilmente podemos hallar la proyección de sobre la horizontal que pasa por . Parece un poco lioso, pero no lo es. Si y entonces:
Una vez tenemos este punto aplicamos la fórmula trigonométrica de la tangete para obtener:
Donde y .
Si definimos así el ángulo tendremos que los cuatro ángulos representados en esta imagen tendrán el mismo valor:
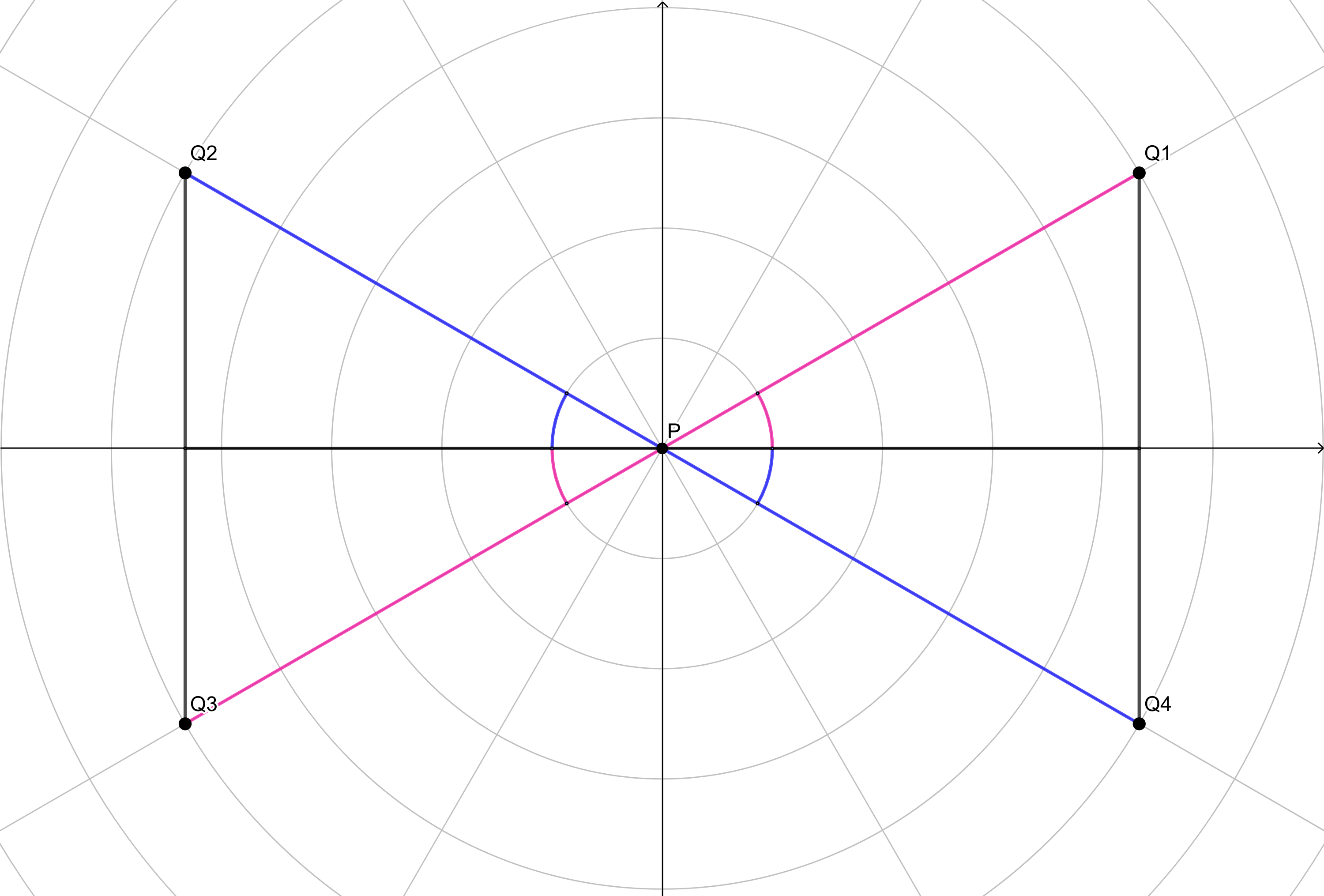
Pero claramente sólo nos interesa que coincidan por una parte los ángulos marcados en azul y por otra los marcados en rosa, así que debemos diferenciar ambos casos.
Definimos el ángulo como acabamos de explicar:
def angle(p1, p2, q1, q2):
if q1 == p1:
return np.pi / 2
d1 = abs(p1 - q1)
d2 = abs(p2 - q2)
angle = np.arctan2(d2, d1)
return angle if p1 < q1 and p2 < q2 or p1 > q1 and p2 > q2 else -angle
Creamos una función auxiliar que utilizaremos para agrupar todos los puntos que comparten ángulo entre ellos. Los devolveremos en el mismo formato que en el método anterior, para facilitar la representación gráfica.
def group_by_angle(angles, p):
colinear = [[angles[0]]]
count = 0
for angle in angles[1:]:
if angle[1] == colinear[count][0][1]:
colinear[count].append(angle)
else:
colinear.append([angle])
count += 1
colinear = [[c[0] for c in line] for line in colinear if len(line) > 1]
x_values, y_values = [], []
for line in colinear:
for point in line:
x_values += [p[0], point[0]]
y_values += [p[1], point[1]]
return x_values, y_values
Por último implementamos el algoritmo en sí, en este caso vemos que sólo tenemos un bucle anidado y la ordenación de la lista como hemos explicado antes.
def colinear_2(x_values, y_values):
size = len(x_values)
x_coord, y_coord = [], []
for i in range(size):
p_angles = []
x_p, y_p = x_values[i], y_values[i]
for j in range(size):
if i == j:
continue
x_q, y_q = x_values[j], y_values[j]
p_angles.append([(x_q, y_q), angle(x_p, y_p, x_q, y_q)])
# Ordenando la lista por angulo
p_angles = sorted(p_angles, key=lambda x: x[1])
x, y = group_by_angle(p_angles, (x_p, y_p))
x_coord += x
y_coord += y
return x_coord, y_coord
Ejecutemos y comprobemos si los resultados son los esperados (los mismos que los obtenidos en el primer método).
x, y = colinear_2(x_values, y_values)
# Showing the results
for i in range(0, len(x), 2):
_ = plt.plot(x[i:i + 2], y[i:i + 2], c='Tomato', alpha=0.7)
_ = plt.scatter(x_values, y_values, c=colors, cmap='hsv', alpha=0.7)
plt.show()
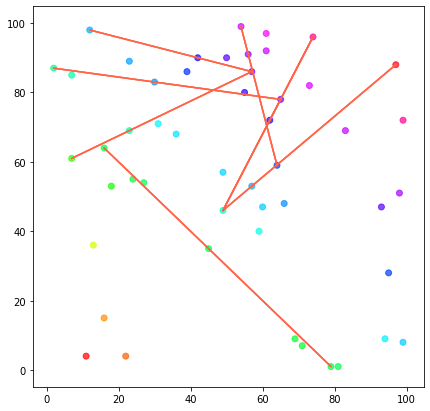
Observamos que la salida es la misma que para el método 1. A la hora de ejecutar se percibe que este método es ligeramente más rápido, comprobemos si esto es cierto.
Midiendo tiempos
Veamos ahora el rendimiento de cada uno de estos métodos. Para ello vamos a generar conjuntos de puntos de diferentes tamaños, y para cada uno de ellos mediremos el tiempo de ejecución de cada método.
sizes = np.linspace(start=10, stop=200, num=20)
t_method1 = []
t_method2 = []
for n_points in sizes:
n = int(n_points)
x_values = [np.random.randint(100) for i in range(n)]
y_values = [np.random.randint(100) for i in range(n)]
start = time.time()
colinear_1(x_values, y_values)
end = time.time()
t_method1.append(end - start)
start = time.time()
colinear_2(x_values, y_values)
end = time.time()
t_method2.append(end - start)
line1 = plt.plot(sizes, t_method1, color='purple', label='Method 1')
line2 = plt.plot(sizes, t_method2, color='Tomato', label='Method 2')
plt.legend(loc='upper left')
plt.xlabel('Number of points')
plt.ylabel('Execution time (s)')
plt.title('Method 1 vs. Method 2 Execution time')
plt.show()
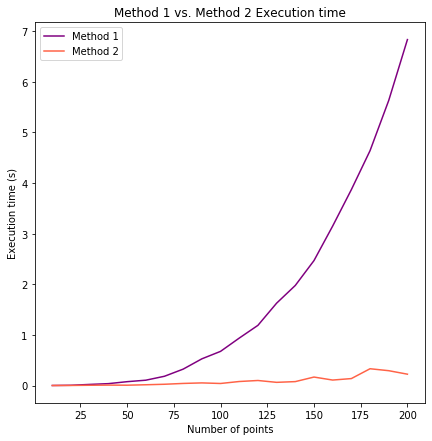
De esta forma estamos comprobando experimentalmente que el coste del método 1 es mucho mayor al del método 2 para tamaños grandes del conjunto de entrada. A partir de conjuntos de más de 50 puntos las diferencias entre ambos métodos son notables, superando en varios segundos los tiempos de ejecución.
Materiales
Como en otras ocasiones os dejo el enlace al repositorio de GitHub del blog, en él encontraréis el código explicado en el post y todo lo que he utilizado para realizar las animaciones.